- 需要做例题巩固!
参数检验:假设数据满足正态性、方差齐性、独立性等假设,通过估计总体参数(均值、方差等)进行检验。常见的如 z 检验、t 检验、方差分析等。
而非参数检验则不依赖总体分布假设(当然也就不涉及总体参数),适用于非正态、等级数据或小样本。常见的如游程检验、秩和检验、符号检验、符号秩检验、中位数检验和弗里德曼检验等。
采用非参数检验的原因是,多数情况我们往往并不知道总体的分布。
游程检验 run test
针对样本随机性的检验。随机性的重要性:①代表总体;②减轻噪声因子影响。
假设某随机变量有X和Y两种状态,那么连续的X或者连续的Y称为一个游程(run,即连续的相同事件), 如对于序列 $(XX)(Y)(X)(YY)(XXX)$ 有 $R_x=3, R_y=2, R=5$.
假如不止两种状态,可以使用多类别游程检验。
对于完全随机数据,$R$ 既不会太大,也不会太小。
- 小样本量情形 $R_x<20, R_y<20$,使用精确法。根据 x 样本个数和 y 样本个数 $n_1, n_2$ 即可查表得 $R$ 的临界值,从而做出决策。(注意查表用的是 $n_1, n_2$, 不是 $R_x, R_y$ !)
- 大样本情形 $R_x+R_y>40$:$R$ 的分布可用正态分布近似。
 图源 统计学与质量036 - 非参数检验(Non-Parametric) - 游程检验(Run Test)
图源 统计学与质量036 - 非参数检验(Non-Parametric) - 游程检验(Run Test)
即使是连续型数据,也可做游程检验。根据中位数将数据划分为两类即可。
符号检验 sign test
符号检验法是通过两个相关样本的每对数据之差的符号进行检验,从而比较两个样本的显著性。具体地讲,若两个样本差异不显著,正差值与负差值的个数应大致各占一半。 符号检验与参数检验中配对样本t检验相对应,不满足参数检验条件时,可采用此法来检验两相关样本的差异显著性。
广义符号检验是对连续变量任意分位点 $x_{n}$ 进行的检验,而狭义的符号检验则是针对中位数 $M= Q_{0.5}$ 进行的检验。
大于临界值的记为 $S^+$, 小于临界值的记为 $S^-$, 使用二项分布计算 p 值,然后与显著性水平比较即可完成检验。
精度低,易犯第二类错误(pmf 的锅)
Wilcoxon 符号秩检验
威尔科克森符号秩检验,计算的是样本与中位数之差/两匹配样本之差…绝对值的秩,的正和和负和。如果它们有相同的样本点,每个点取平均秩。在零假设下,$W^+$ 和 $W^-$ 应差不多
把观测值和零假设的中心位置之差的绝对值的秩分别按照不同的符号相加作为其检验统计量。临界值参考秩和表。
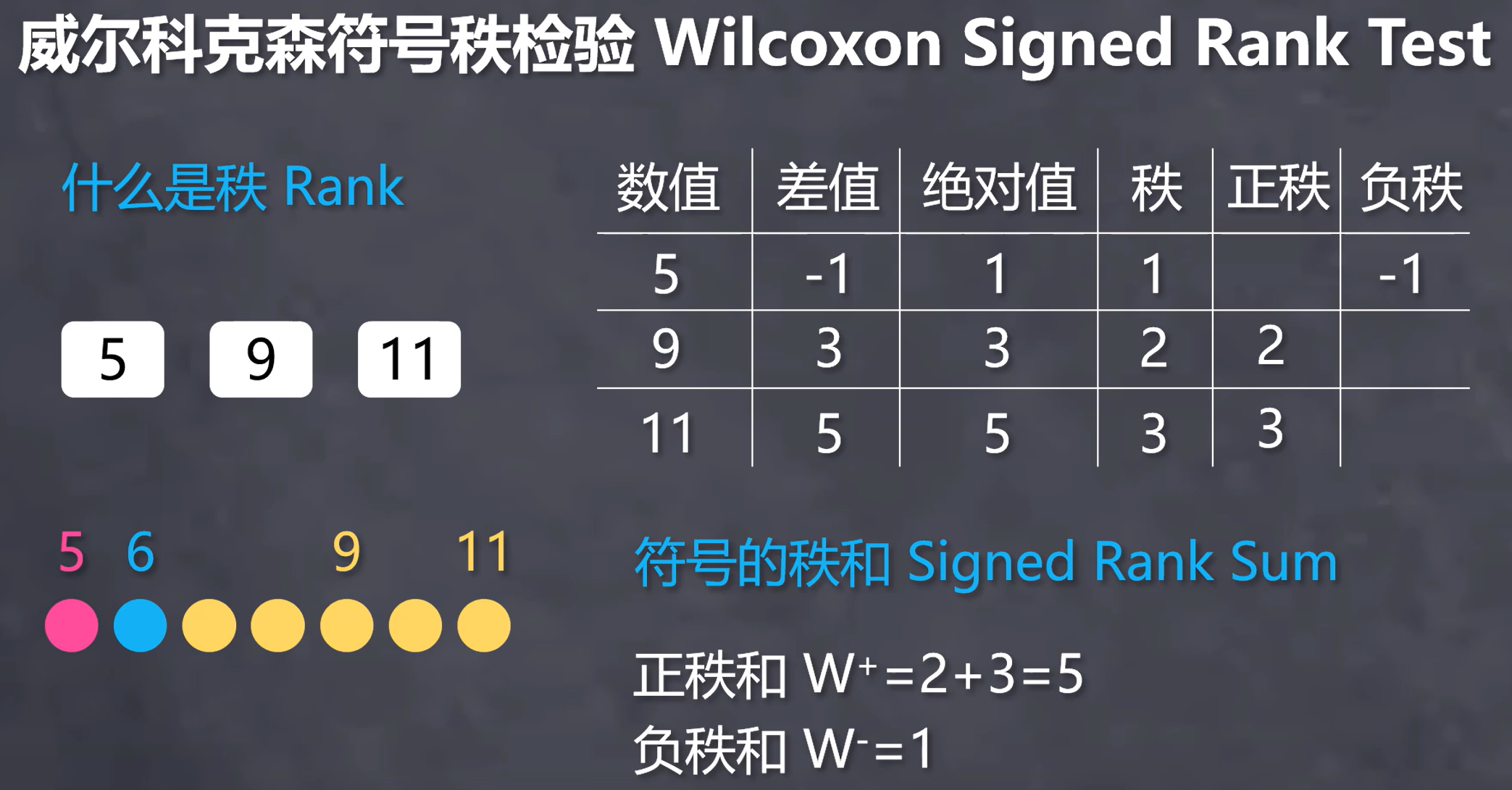 图源 统计学与质量038 - 非参数单样本中位数 - 符号秩检验(Signed Rank Test)
图源 统计学与质量038 - 非参数单样本中位数 - 符号秩检验(Signed Rank Test)
...