茎叶图
优点:
- 直观展示数据分布:茎叶图通过将数据分成“茎”和“叶”两部分,能够直观地展示数据的分布情况。
- 保留原始数据:与直⽅图不同,茎叶图保留了原始数据的详细信息,每个数据点都可以从图中直接读取。
- 简单易绘制:茎叶图不需要复杂的计算或⼯具,⼿⼯即可快速绘制。
- 适合⼩数据集:茎叶图特别适合展示⼩数据集,能够清晰地显示每个数据点的位置。
缺点:
- 茎叶图只便于表示两位有效数字的数据;
- 茎叶图只方便记录两组的数据;
- 茎叶图不适用于大数据集。
作⽤:
- 数据探索:在数据分析的初期,茎叶图可以帮助快速了解数据的分布和集中趋势。
- 异常值检测:通过观察茎叶图,可以很容易地发现数据中的异常值或离群点。
- 数据⽐较:可以绘制多个茎叶图来⽐较不同数据集之间的分布情况。
茎叶图优化?
直方图
由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型,纵轴表示分布情况。
优点:
- 直观展示数据分布
- 适用于大规模数据集
- 可以通过多个直方图对比不同数据集的分布差异。
缺点:
- 丢失数据原始信息
- 绘制复杂
作用:
- 数据探索:直观感受的集中趋势、离散程度、偏态和峰态;发现数据的模式,比如是否呈正态分布、偏态分布或多峰分布。
- 识别异常值,发现数据中的极端情况。
条形图(柱状图)Vs 直方图:
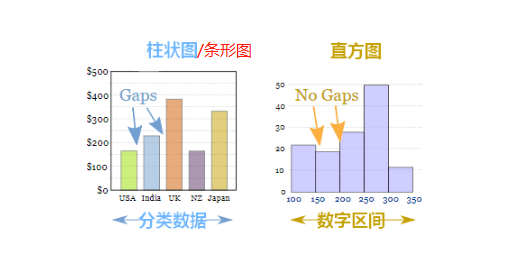
直方图 Vs 经验分布函数 Vs 概率密度函数:直方图和经验分布函数之间没什么关系;重点写一下直方图和概率密度函数之间的关系:直方图表示一个变量的值在范围内的概率,直方图是离散化的 pdf, pdf 是连续化的直方图(想象直方图的区间越来越小、越来越密。感觉有点微积分的味道?)
箱线图
优点:
- 方便多组数据比较;
- 识别异常值;
- 使用数据量大的情形
缺点:
- 丢失数据原始信息
- 对数据量较少的情况不够直观
- 不适用小数据情形
作用:
- 直观展示数据的分布特征(如中位数、四分位数、离散程度)。
- 识别异常值,帮助发现数据中的极端值。
- 便于对比多个数据集的分布差异,尤其适用于数据间的偏态比较。
改良版的箱线图:增加上下限阈值。四分位间距 $IQR = Q3 - Q1$, 上限阈值:$Q3 + 1.5 \times IQR$, 下限阈值:$Q1 - 1.5 \times IQR$;超出上述阈值的点定义为疑似异常值,并在图中标注(如用星号表示)
...