随机事件层面的独立
在概率论里,“独立"并不意味着两个事件没有任何关系。 独立意味着一个事件的发生与否都不改变另一个事件发生的概率。 - 知乎文章
数学定义见下:
两个随机事件间的独立性定义: $P(AB)=P(A)P(B)$,即 $P(A|B)=P(A)$ 。不独立,又称相依。
多个随机事件间的独立性定义:设有 N 个事件 $A_1, A_2, …, A_N$ 对任意的 $1 ≤ i ≤ j ≤ k ≤ N$ 如下式成立:为什么不使用 $i, j, k \in [1, N]$ ?避免重复吗?
$$ \begin{aligned} P(A_i A_j) &= P(A_i) P(A_j) \quad \text{两两独立} \\ P(A_i A_j A_k) &= P(A_i) P(A_j) P(A_k) \quad \text{三三独立} \\ &\quad \vdots \\ P(A_i A_j \cdots A_N) &= P(A_i) P(A_j) \cdots P(A_N) \quad \text{NN独立} \end{aligned} $$ 则称 N 个事件 $A_1, A_2, …, A_N$ 相互独立。
多个事件间相互独立 <=> 多个事件间两两独立、三三独立、……、NN 独立
概率为 0 的事件与任何事件都独立。
将相互独立事件中的任一部分转换为对立事件,所得诸事件依然是相互独立的。
如若事件 A 与事件 B 独立,则 $A$ 与 $\bar{B}$, $\bar{A}$ 与 $\bar{B}$, $\bar{A}$ 与 $B$ 均独立。
多个随机事件情形同样满足
随机试验层面的独立

独立性与相容性
相容性定义:如果 A 与 B 没有相同的样本点,则称 A 与 B 互不相容。即 A 与 B 不可能同时发生。
在事件概率不为 0 的前提下讨论独立性与相容性的关系:
- 独立 => 相容:$P(AB)=P(A)P(B)≠0$ 说明 A 与 B 之间有交集,两者可能同时发生;但反之则不成立:相容事件不一定独立,例如掷一枚骰子,A: 点数<4 , B: 点数>3,AB 有交集,两者可能同时发生,相容,但不独立。
- 逆否命题:互不相容 => 相依(不独立),互不相容 => $P(AB)=0≠P(A)P(B)$ 说明 A 与 B 不独立。反之同样不成立:相依事件可能相容,例如掷两枚骰子,A:第一次为 6,B:总和大于 8,AB 两事件既相容又相依。
独立性:概率层面,反映前后实验结果是否相互影响; 相容性:事件层面,反映不同事件能否同时发生。
可以说,两者其实是不同维度的概念。
独立性与相关性
不相关是指两个变量的相关系数为0,$E(XY)=E(X)E(Y)$,两个变量之间没有线性关系。
相关与否,仅是线性层面的。而独立与否,不仅包括线性层面,还包括非线性层面。
相关性是用矩来定义的,矩只能反映线性层面的关系;而独立性是用分布定义的,独立意味着信息/变量可分离,不仅包括线性层面的分离,还包括非线性层面的分离,条件更强。于是可以说:独立的要求,比不相关,要更加严格。
- 独立 => 不相关,反之不成立,事件间不相关(无线性关系)≠> 事件间独立(可能存在非线性关系)
- 逆否命题:相关 => 相依,反之同样不成立,相依(不独立,说明事件间有关系)≠> 相关(因为可能不是线性关系,而是非线性关系)
拓展 Spearman 相关系数和 Kendell 相关系数
Spearman 相关性的基本思想是:分别对两个变量X、Y做等级变换(rank transformation),用等级 $R_x$ 和 $R_y$ 表示;然后按Pearson相关性分析的方法计算 $R_x$ 和 $R_y$ 的相关性。$\rho = 1 - \frac{6 \sum_{i=1}^{N} d_i^2}{N(N^2 - 1)}$. 其中 $d_i$ 表示两个变量分别排序后成对的变量位置差,N 表示 N 个样本,减少异常值的影响。
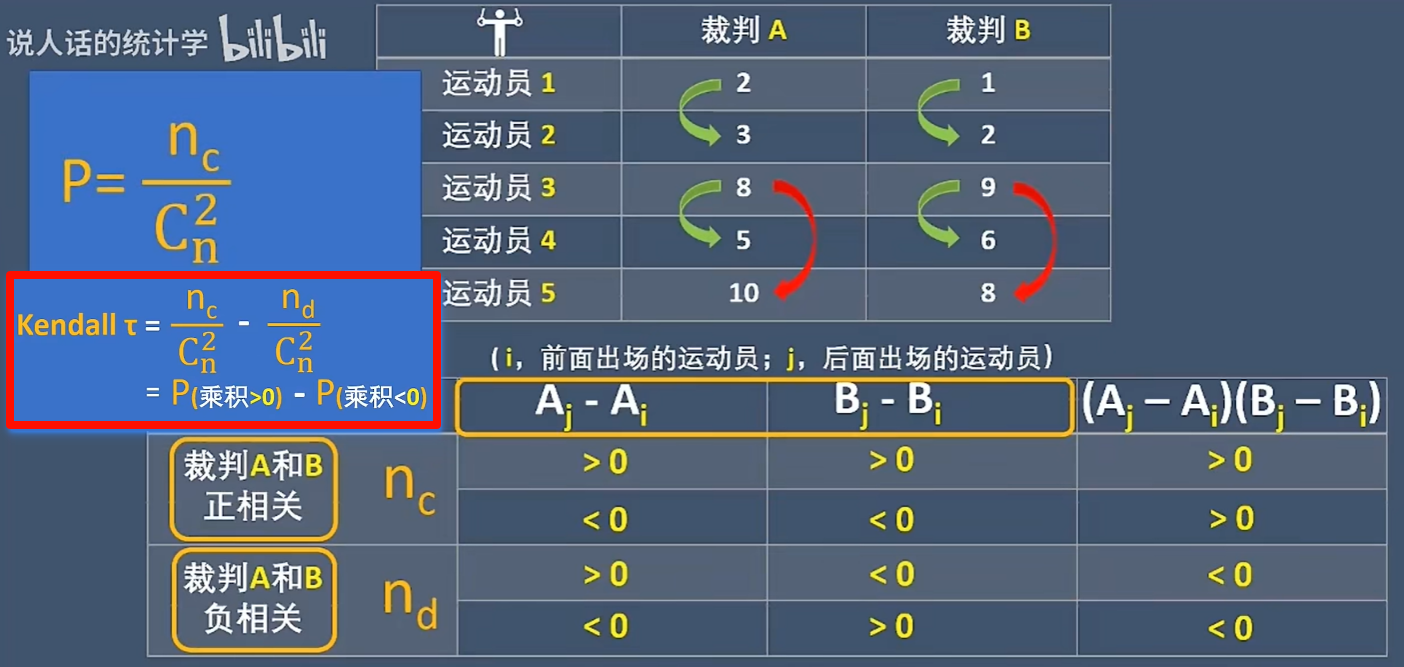
Kendell 相关系数:是一种非参数统计指标,用于衡量两个变量之间的排序一致性,即它们的相对排名是否一致。它特别适用于判断两个变量是否具有单调关系,而不要求线性关系。
假设有两个变量 X 和 Y,分别对应 n 个观测值的排名:$(X_1, Y_1), (X_2, Y_2), …, (X_n, Y_n)$, 我们对所有可能的数据点对 $(X_i, Y_i)$ 和 $(X_j, Y_j)$ 进行比较:
- 一致对(Concordant pairs): 如果 $X_i > X_j$ 且 $Y_i > Y_j$(或 $X_i < X_j$ 且 $Y_i < Y_j$),则称为一致对,表示两者排序方向相同。
- 不一致对(Discordant pairs): 如果 $X_i > X_j$ 且 $Y_i < Y_j$(或 $X_i < X_j$ 且 $Y_i > Y_j$),则称为不一致对,表示两者排序方向相反。
- 平局对(Tied pairs): 如果 $X_i = X_j$ 且 $Y_i = Y_j$,则称为平局。如存在平局对则需要进行修正(具体如何修正略)。
计算 Kendall 相关系数,可以使用 Python 的 scipy.stats.kendalltau:
1from scipy.stats import kendalltau
2
3X = [1, 2, 3, 4]
4Y = [2, 1, 3, 4]
5tau, p_value = kendalltau(X, Y)
6
7print(f"Kendall's tau: {tau}, p-value: {p_value}")
拓展施瓦茨不等式
如何理解施瓦茨不等式?

...