假设检验是统计推断的重要方法!统计推断包括假设检验和参数估计。
假设检验的定义
假设检验(hypothesis testing)是指从对总体参数所做的一个假设开始,然后搜集样本数据,计算出样本统计量,进而运用这些数据测定假设的总体参数在多大程度上是可靠的,并做出承认还是拒绝该假设的判断。如果进行假设检验时总体的分布形式已知,需要对总体的未知参数进行假设检验,称其为参数假设检验;若对总体分布形式所知甚少,需要对未知分布函数的形式及其他特征进行假设检验,通常称之为非参数假设检验。此外,根据研究者感兴趣的备择假设的内容不同,假设检验还可分为单侧检验(单尾检验)和双侧检验(双尾检验),而单侧检验又分为左侧检验和右侧检验。 - 国家统计局
所谓假设检验,就是通过样本来推测总体是否具备某种性质。
若假设可用一个参数的集合表示, 该假设检验问题称为参数假设检验问题, 否则称为非参数假设检验问题。 - 其它地方看到,感觉怪怪的。
假设检验的原理
假设检验使用的是“证伪”的思想,是一种“反证法”。
假设检验的基本思想是反证法思想和小概率事件原理。 反证法的思想是首先提出假设(由于未经检验是否成立,所以称为零假设、原假设或无效假设),然后用适当的统计方法,根据已有的样本,来确定假设成立的可能性大小,如果可能性小,则认为假设不成立,拒绝它;如果可能性大,还不能认为它不成立。
小概率事件原理,是指小概率事件在一次随机试验中几乎不可能发生,小概率事件发生的概率一般称之为“显著性水平”或“检验水平”,用 $\alpha$ 表示,而概率小于多少算小概率是相对的,在进行统计分析时要事先规定,通常取 $\alpha=0.01、0.05、0.10$ 等。 - 国家统计局
🤯反证法是数学上的严格证明方法,结论绝对正确;而假设检验属于统计学范畴,结论具有一定的概率风险,因此不一定正确。
假设检验具体是如何操作的?
- 代入给定的 $H_0$ 的参数值建立分布
- 看看样本“像不像”是从这个分布里头出来的(是否落入拒绝域)
- 若“像”(落入接受域),这帮样本就是从 $H_0$ 那个分布来的,说明 $H_0$ 对应的参数有可能就是真实参数;
- 若“不像”(落入拒绝域),好家伙这帮样本不是从 $H_0$ 那个分布来的,说明 $H_0$ 对应的参数大概率不是真实参数(拒绝 $H_0$)。但是 $H_0$ 错误,不代表 $H_1$ 就正确,所以只能说“拒绝 $H_0$”,而不能说“接受 $H_1$”)
- 如何量化这个“像”与“不像”,详见后面关于显著性水平 $\alpha$ 和 P-value 的章节。
- Over 下结论。
知道了假设检验具体是如何操作的,也就知道了:
为什么假设检验要将等号放在原假设?
因为检验统计量的计算需要给定一个(假想的)参数值,否则就无法建立相应的分布,不方便计算。比如说,简单的单总体均值检验中,假定 $H_0: \mu = 20$ 这样才能简单地把确定在这个假想均值确定的抽样分布下,把检验统计量给算出来。不带等号的话,这个分布的确定就困难了。
假如,我偏不把等号放在原假设,把不等号放在原假设,例如 $H_0: \mu < 20$ 我取 $\mu$ 等于多少来建立分布呢?是 19?还是 15?亦或是 10?这时不就出现问题了。
关于检验统计量的选取
分布是个好东西!
The statistical models of distributions, however, enable us to describe the mathematical nature of that randomness. - 《The lady tasting tea》
Eg. 现有一关于参数 $\theta$ 的假设检验:理论上只要某统计量 T 的分布与参数 $\theta$ 有关,即可用它来构造检验统计量。
因为如果我们能得到 $H_0$ 成立下统计量 T 的分布,即可计算出在该分布中出现样本或其它更极端情况的概率。
关键是:分布!
- 检验统计量的选取 - 这个地方可以想个例子来帮助理解。 ✅ 2025-03-14
举个例子:考虑两样本量分别为 n, m 的独立正态总体,样本方差比检验 $H_0:\sigma_1^2=\sigma_2^2 \quad Vs \quad H_1:\sigma_1^2 > \sigma_2^2$. 此处使用下分位数。
- 检验统计量 $T_1=\frac{s_1^2}{s_2^2}=10$, 拒绝域 $W_1={T_1≥F_{1-\alpha}(n-1, m-1)}$.
- 检验统计量 $T_2=\frac{s_2^2}{s_1^2}=0.1$, 拒绝域 $W_2={T_2≤F_{\alpha}(m-1, n-1)}$.
- 可以看到,选择不同的检验统计量,所构造出来的拒绝域的方向也不同!所以在实际假设检验中,对于“拒绝域的方向一般与 $H_1$ 方向相同”这样的结论要慎用。
⚠️区分统计量和枢轴量(检验统计量也是统计量):
- 统计量不含参,但统计量的分布含参;如 $\bar{X} \sim N(\mu, \frac{\sigma^2}{n})$;
- 枢轴量含参,但枢轴量的分布不含参。如 $Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$. 枢轴量主要用于区间估计和假设检验中。
假设检验的精髓:不平衡(Imbalance)
假设检验中,原假设 $H_0$ 和备择假设 $H_1$ 的地位是不对等的:
- $H_0$ 通常是被默认为真的假设,需要足够的证据才能拒绝;
- 而 $H_1$ 则与 $H_0$ 相对立,通常是研究者试图去证明的假设。
打个比方:
- $H_0$ 像是“正统”,“权威”,“传统”,具有一定的“优先权”,默认情况下它都是正确的
- 而 $H_1$ 则像是“新教”,“创新”,甚至有些“备胎”的味道,需要在将 $H_0$ 拒绝后,才可能“喧宾夺主”,有“翻身”的机会。这里使用的“可能”、“机会”两词是严谨的,因为在实际的假设检验中:
- 哪怕拒绝了原假设,我们会说在 xx 的显著性水平下能够“拒绝 $H_0$”,而不是“接受 $H_1$”;
- 同样若没拒绝原假设,我们会说在 xx 的显著性水平下不能“拒绝 $H_0$”,而不是“接受 $H_0$”。
- 总结:判断一个假设是否『正确』是很难的,然而判断一个假设是否『错误』相对来说就容易多了:因为证伪只需要一个特例就足够了,一个特例足以推翻一个论点,却远远不能支撑一个论点。
之所以如此不平衡地设计“假设检验”这个东西,是为了给原假设一定“优先权”,这样有助于控制做出错误结论的风险(特别是第一类错误)。打个比方:“传统”的 $H_0$ 一般都是正确的,为防止左倾冒进分子冲动地推翻,于是在设计上给了它(即 $H_0$ )一定的“优先权”。(备胎想要成为上位?很难的啦)
矛盾无处不在,这种“不平衡”的设计,同样具有双面性:虽然确实有助于控制做出错误结论的风险,但如此不平衡的设计导致它并非使用于所有问题。如:
现有一堆 0-2 之间的样本,判断是来自 $U(0, 1)$ 还是 $U(1, 2)$ 。这个问题就不适用于假设检验。因为在这个问题中 $U(0, 1)$ 和 $U(1, 2)$ 的“地位”是平等的。可通过极大似然估计 MLE 来解决这个问题。(分别计算样本在 $U(0, 1)$ 和 $U(1, 2)$ 的对数似然值即可,看哪个大)
而像女士品茶(将牛奶倒入茶和将茶倒入牛奶对奶茶的口味是否有影响)这样的问题,显然是能够根据我们的先验知识做出一定猜测的,这种问题便可以通过假设检验这样的方法来解决。
通过了解如何做出原假设,能够帮助你更好地理解假设检验的 Imbalance.
做出原假设的依据
- 根据现有理论或知识:原假设往往基于现有的理论或广泛接受的知识。例如,如果现有理论表明两种药物效果相同,那么原假设可能就是"这两种药物的效果没有差异”。
- 简单性或保守性:在统计学中,原假设通常是一个简单假设,它提出了最简单、最保守的情况。例如,“新药与安慰剂效果无差别”是一个比“新药比安慰剂效果好”更简单、更保守的假设。
- 研究目的:研究者可能会根据研究目的来确定原假设。如果研究目的是证明一种新的干预措施有效,那么原假设可能就是“新干预措施与现有措施效果相同”。
那么问题来了:如何理解交换 $H_0$, $H_1$ 导致的检验结果变化呢?体会其中的“不平衡”
交换 $H_0$ 和 $H_1$, 检验的方向发生了改变,就代表研究者的立场发生了改变,这样做将导致就同一样本数据得到的结论可能相同、但也可能相反。也就是:虽然数据还是来自于同个样本同样的数据,但原先用来支撑先前观点的论据,这时候可能就用来打脸了。
显著性水平 $\alpha$ 与功效 $1-\beta$ 与 P-value
| 项目 | 无法拒绝 $H_0$ | 拒绝 $H_0$ |
|---|---|---|
| $H_0$ 为真 | $1-\alpha$ | $\alpha$ 弃真错误 |
| $H_0$ 为伪 | $\beta$ 取伪错误 | $1-\beta$ 功效 |
用极限的思想来理解:在固定样本量的前提下,不能同时减小第一类错误 $\alpha$ 和第二类错误 $\beta$ :
- 若 $\alpha=0$ -> 不犯弃真错误 -> 索性直接接受原假设 -> 更有可能犯 $\beta$
- 若 $\beta=0$ -> 不犯取伪错误 -> 索性直接拒绝原假设 -> 更有可能犯 $\alpha$
- 整个实验来看:$\alpha + \beta \in (0, 2)$ ,若某分类器将所有正例均判为负,将所有负例都判为正,这时 $\alpha=\beta=1, \quad \alpha+\beta=2$
- 单次实验结果来看,不可能同时发生弃真错误和取伪错误。表格中的四个值 $1-\alpha, \quad \alpha, \quad \beta, \quad 1-\beta$ 均 $\in (0, 1)$
显著性水平 $\alpha$
在假设检验中,显著性水平(Significance Level),通常记为 $\alpha$,是指在原假设 $H_0$ 为真时,错误地拒绝 $H_0$ 的概率,即第一类错误(Type I Error)的概率。换句话说,$\alpha$ 代表了我们能够接受的犯第一类错误的概率(假阳性风险),即我们错误地发现了一个不存在的效应的可能性。
两类错误,在具体实践中往往更加关注弃真错误 $\alpha$ ,因为错误地拒绝“传统”、“权威”的原假设 $H_0$ (即弃真错误)所带来的损失,相对于在权威假设 $H_0$ 错误的背景下, 没能找到真正正确的假设 $H_1$,仍误认为权威假设 $H_0$ 是正确的(即取伪错误)而言,是更大的。
例如,在制药行业,如果一个新药被批准(拒绝 $H_0$ )但实际上无效或有害,会带来巨大损失;相反,如果一个有效药物未被批准(即犯第二类错误),虽然可惜,但仍可在未来研究中重新评估。
P值 P-value
P-value:在原假设成立的条件下,出现样本或更极端情况的概率。
在假设检验实际操作中,可通过比较 P-value 与显著性水平 $\alpha$ 值的大小比较来判断是否应该拒绝原假设。
举个稍微有点极端的例子:现有样本来自某正态分布 $N(\mu, 0)$ :[8, 17, 10, 9],考虑假设检验问题 $H_0: \mu=0$ Vs $H_1: \mu=10$ 。
我们来看看此时原假设 $H_0: \mu=0$ 成立的条件下出现样本或更极端情况的概率,即从 $N(0, 1)$ 中抽到[8, 17, 10, 9]这几个样本的概率,显然很小,即 P-value 很小,P-value 越小,越是应该拒绝原假设。
想想,咱假设原假设成立,可是发现这个假设下出现我们实际抽到的样本的概率极低,此时理所当然应该拒绝原假设。
P-value 一般都介于 0-1 之间,怎么量化它的“小”呢?这时显著性水平 $\alpha$ 就站了出来,大喊一声“我来!”。可以将显著性水平 $\alpha$ 理解为“阈值”
- 若 P-value <= $\alpha$ ,说明 P-value < 阈值,拒绝原假设
- 反之则不能拒绝原假设
关于 P 值的争议
$p-value = P(T(X)>T(x)|H_0成立)$, 记后验概率 $\alpha_0=P(H_0成立|x)$. 相对于 P 值,后验概率 $\alpha_0$ 更有意义(联系贝叶斯定理,如医学领域假阳性情况)
Lindley 悖论:当样本量足够大时,$\alpha_0$ 可以趋于 1,而 p-value 接近于 0,即利用 P 值检验和贝叶斯检验得到的结果相悖。而贝叶斯检验中后验概率的计算需要依赖先验分布的主观假定,(其实经典假设检验中的显著性水平 $\alpha$ 也是人为主观设定的)这就引起了经典假设检验和贝叶斯假设检验的重要争议。
P-值一般过于高估拒绝 $H_0$ 的证据,尤其在大样本情况下更容易出现显著差异,大样本情形下抽样结果与 $H_0$ 的微小差别,就能得到一个极小的 P 值,易犯拒真错误。
所以在某些特定的情况下,贝叶斯检验法较 P 值检验法具有一定的优越性。参考 P值的局限性 & 贝叶斯假设检定
功效 Power $1-\beta$
另外一个稍微“小众”一些的概念 - 功效(Power):反映检验在面对正确的备择假设时正确做出决定的能力。有点像“抓走坏人”的能力。毫无疑问,越大越好。
再延伸一个更“小众”的概念 - 势函数 / 功效函数 (Power Funtion):功效函数(Power Function)是用于衡量检验方法在不同实际参数值下拒绝原假设的概率。即不同实际参数值下样本观测值落入拒绝域内的概率。综合反映了第一类错误和功效的情况。
$$ g(\theta) = \begin{cases} \begin{array}{rl} \phantom{1 -} \alpha(\theta), & \theta \in \Theta_0 \\ 1 - \beta(\theta), & \theta \in \Theta_1 \end{array} \end{cases} $$
当 $H_0$ 为真时,$g(\theta)$ 为犯第一类错误的概率 当 $H_1$ 为真时,$g(\theta)$ 为功效
既然固定样本容量时,任何检验都不能同时让第一类错误和第二类错误的概率很小,那么 (Jerzy) Neyman-(Egon) Pearson 所提出的原则就是:在保证犯第一类错误的概率不超过指定数值 $\alpha$ 的检验中,寻找犯第二类错误 $\beta$ 概率尽可能小的检验。(N-P准则)
N-P 准则用势函数 / 功效函数(Power Function)来表达: $$ \begin{cases} g(\theta) \leq \alpha, & \theta \in \Theta_0 \\ g(\theta) \text{ 尽可能大}, & \theta \in \Theta_1 \end{cases} $$ 势函数的作用:

如何评价某个假设检验的好坏
- 显著性水平 $\alpha$,与第一类错误相关联;
- 功效 $1-\beta$, 与第二类错误相关联;
- 假设条件的严苛性,与稳健性相关联。
- 计算复杂度
假设检验与区间估计的关系
24北师应统真题,茆P326
区别 1:
- 假设检验是判断一个有关总体未知参数的命题是否成立的问题,且只能证伪;
- 而区间估计是构造一个未知参数最合理的取值范围的问题。
- 区间估计所提供的信息要比假设检验更加丰富。
区别 2:值得细品🤔
- 置信区间是针对参数的集合,置信区间是用来估计参数的,这个很好理解;
- 拒绝域与接受域是针对样本的集合,拒绝域+接受域=样本空间。
区别 3:
- 区间估计求得的是以样本估计值为中心的双侧置信区间
- 假设检验既有双侧检验,也有单侧检验;
区别 4:这和区别 1 是一脉相承的,立足于大/小概率,取决于从正面(证实)/反面(证伪)来看待问题。
- 区间估计立足于大概率,通常以较大的把握程度(可信度)1-α 去估计总体参数的置信区间;
- 假设检验立足于小概率,通常是给定很小的显著性水平α 去检验对总体参数的先验假设是否成立。
联系:
- 拒绝域与置信区间的对偶关系:
- 双侧检验问题的接受域即置信区间
- 单侧检验问题的接受域即置信上/下限,例单侧检验 $H_0:\mu≤\mu_0 \quad vs \quad H_1:\mu>\mu_0$, 其接受域 $W={u=\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}≤z_{1-\alpha}}$, 移项: $\mu≥\bar{x}-z_{1-\alpha}\frac{\sigma}{\sqrt{n}}$. 便得到了参数 $\mu$ 的 $1-\alpha$ 置信下限。
- 都是根据样本信息推断总体参数,以抽样分布为理论依据,建立在概率论基础之上的推断,推断结果都有风险;
其它
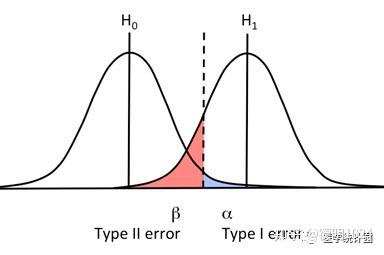
其它条件不变的前提下,增大样本量,会使 $\alpha$ 和 $\beta$ 同时减小吗?争议问题🤔
| 会 | 不会 目前占上风 |
|---|---|
| 显著性水平是人为给定,但犯第一类错误 $\alpha$ 的概率不是恒定的,它会受样本量和犯第二类错误 $\beta$ 的概率等影响。 ——贾俊平《统计学》和我的概率论老师 |
增大样本量,只能降低犯第二类错误 $\beta$ 的概率(提升功效,因为随着样本量↑,估计精度↑),而犯第一类错误的概率是由人为设定的显著性水平 $\alpha$ 来决定的,无法通过增大样本量来降低。 ——《卫生统计学第八版》和 GPT,以及 DeepSeek |
选择合适的检验⽅法或改进实验设计,可以在⼀定程度上优化两类错误的平衡。例如,使⽤更⾼效的统计模型或增加实验的灵敏度。
两个正态总体均值差的检验
参考国家统计局网页
- 方差已知:u 统计量
- 方差未知情形,我们需要先做⼀个⽅差⻬性检验,来判断两个总体的⽅差是否相等。
- 方差相等但未知:Student’s t-test, 带 $Sw$ 的那个公式
- 方差不等且未知:Welch’s t-test,使用 Satterthwaite 公式计算自由度
- 非正态总体:
- 小样本:Mann-Whitney U 检验(也称为 Wilcoxon 秩和检验)
- 大样本:近似正态
- 其它非参数检验方法:Bootstrap ⽅法、置换检验……
单正态总体均值的检验,方差的检验和方差比的检验暂略。
...